Report by PhD, (associate) professor at the Uppsala University, Sweden (Division of Scientific Computing, Department of Information Technology) and Texas A&M University (USA) Nazarov M. on the topic “Viscous Regularization of the MHD Equations”.
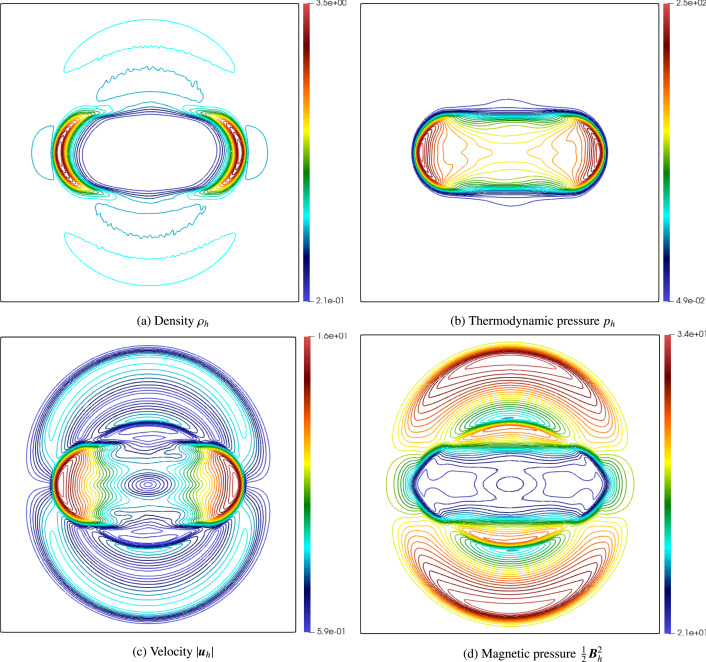
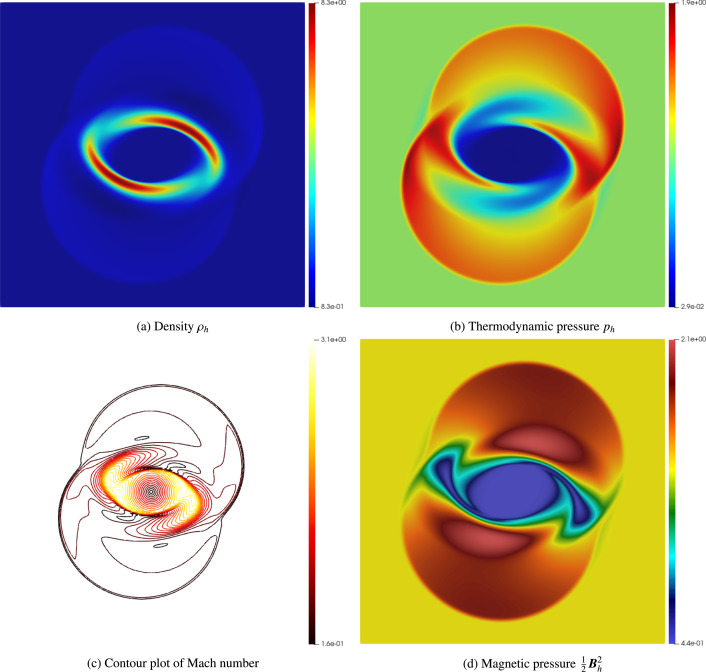
Nonlinear conservation laws such as the system of ideal magnetohydrodynamics (MHD) equa- tions may develop singularities over time. Viscous regularization is a common approach to avoid such situations while obtaining a convergent solution sequence. This talk presents a new viscous flux to regularize the MHD equations. Our proposed viscous flux combines the Guermond-Popov flux [Guermond-Popov, 2014] for compressible flows and the resistivity flux for the magnetic component. We prove that the proposed viscous flux holds attractive properties such as it pre- serves the positivity of density and internal energy, it satisfies the minimum entropy principle, it is consistent with all the generalized entropies, and it is Galilean and rotationally invariant. The proposed viscous regularization has numerically experimented with an artificial viscosity finite element method. The numerical results show that: (i) high-order accuracy is obtained for smooth solutions; (ii) shocks and other discontinuities are finely captured; (iii) the numerical behaviors are strongly aligned with the continuous analysis; (iv) the proposed viscous flux behaves similarly to the resistive MHD flux in the magnetic reconnection test with physical viscosity [1].


Reference
1. Tuan Anh Dao, Murtazo Nazarov. Monolithic parabolic regularization of the MHD equations and entropy principles // Computer Methods in Applied Mechanics and Engineering Volume 398, 1 August 2022, 115269.